|
jueves, octubre 14, 2010
|
||
 He aquí una de las pruebas matemáticas más asombrosas que incluso a los más experimentados en matemáticas deja perplejos (y que acá podrá entender cualquier persona que sepa lo más básico del álgebra): El número 0.9999... es idéntico al número 1. He aquí una de las pruebas matemáticas más asombrosas que incluso a los más experimentados en matemáticas deja perplejos (y que acá podrá entender cualquier persona que sepa lo más básico del álgebra): El número 0.9999... es idéntico al número 1.He aquí la prueba desde dos puntos de vistas distintos:
Como pueden observar, literalmente el número aparentemente infinito 0.9999999... es en realidad el número 1. Y no solo eso, sino que esto ha sido demostrado utilizando todo tipo de formas matemáticas y herramientas, inclusive con formas de números alternativos. El truco está en entender que existe más de una forma de representar un número, y que lo que vemos como 0.999999999... no es más que un símbolo que representa en realidad el número 1. Pero no crean que por simplemente yo escribir el párrafo anterior que soy ningún genio matemático, a mí mismo este dato me dejó tan sorprendido la primera vez que lo vi como estoy seguro los dejará a varios de ustedes ahora mismo, en particular los aficionados a las matemáticas que nunca vieron esto antes, y que sin duda (como traté de hacerlo yo) tratarán de encontrar algún "truco" que invalide esto en las pruebas acá presentadas... :) Lean más respecto a este tema en este enlace en Wikipedia en inglés autor: josé elías |
||
|
|
||
|
|
||
|
Comentarios
Añadir Comentario |
en camino a la singularidad...
©2005-2025 josé c. elías
todos los derechos reservados
como compartir los artículos de eliax
Seguir a @eliax

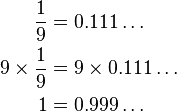
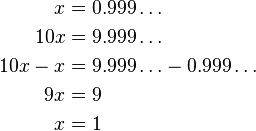
..